Примеры центральной симметрии, Осевая и центральная симметрия
Осевая симметрия часто встречается в повседневной жизни. Не обладают центральной симметрией: угол, произвольный треугольник, трапеция, неправильные многоугольники. Прямоугольный параллелепипед. Прямая призма обладает зеркальной симметрией. Записаться на занятия Записаться на занятия к репетитору.
Пространственное движение — это отображением пространства на себя, которое фиксирует заданные расстояния между определенными точками.
Аналогичным образом будет отображаться и другие геометрические фигуры. К таким можно отнести: треугольник, пирамида, квадрат и другие. Чтобы правильно составить определение центральной симметрии, необходимо вывести понятие симметричности контурных параметров точек относительно друг друга в зависимости от расположения.
Следовательно, точки х и х1 будут называться симметричными относительно заданной координаты О , в том случае, если знание О будет являться центром отрезка х и х1. Центральной симметрией фигуры относительно любой точки будет являться изображение, которое выглядит как фигура, составленная из точек.
В свою очередь эти точки симметричны относительно заданной координаты начальной фигуры. Далее необходимо построить систему координат O zxy. В полученной системе координат ее центром будет являться точка О. Также стоит отметить тот факт, что все эти точки будут симметричны относительно начала координат. Следовательно, расстояние между заданными координатами значений будет определять по следующей формуле:.
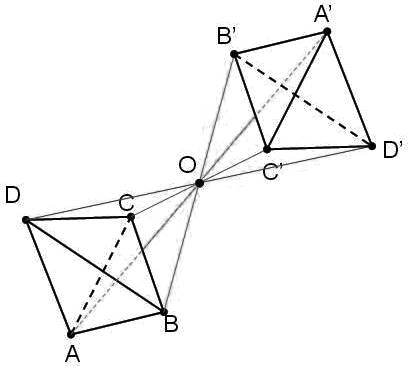
По условию задачи необходимо выполнить построение симметрии центральной симметрии тетраэдра относительно заданных значений и центральной координаты О.
Построение центральной симметрии тетраэдра, относительно точки О, будет выполнено исходя из изображения, которое отражено на рисунке 2. Чтобы выполнить построение центральной симметрии, необходимо для начала провести через все точки геометрической фигуры прямые. Следовательно, центральная симметрия является движением, изменяющим направление на противоположное. Экзамены на носу? Не волнуйся, мы поможем! Регистрируйся на курс подготовки к ЕГЭ по математике и подготовимся к экзаменам вместе!
Центральной симметрией в геометрии обладают параллелограмм, ромб, квадрат, прямоугольник, круг, правильные многоугольники. В повседневной жизни нас также окружают предметы, обладающие центральной симметрией.
Она видна в строении кристаллов и снежинок, которые являются кристаллами льда. Их формы сложные и многообразные, но все они центрально симметричны. В природе это также цветы подсолнух, ромашка, астра и некоторые растения, а в искусстве — необычные орнаменты и строения архитектуры.
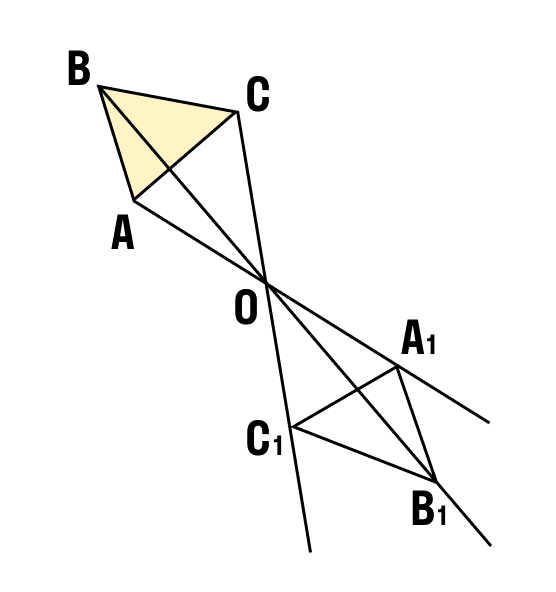
Не обладают центральной симметрией: угол, произвольный треугольник, трапеция, неправильные многоугольники. Дано: прямые а, b и точка О. Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему рис.
Каждая точка прямой а считается симметричной самой себе. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры. Перейти к содержанию wiki. Инструменты пользователя. Инструменты сайта Найти.
Вы находитесь здесь: Wiki: Справочник — EduVdom. Боковая панель Записаться на занятия 47 55 eduVdom. Контакты eduVdom. Оставить отзыв Содержание Центральная и осевая симметрии. Геометрия Справочник Четырехугольники.

Определение четырехугольника. Расстояние между параллельными прямыми. Диагонали и признаки параллелограмма. Теорема Фалеса. Средняя линия треугольника. Пропорциональные отрезки.